https://doi.org/10.61286/e-rms.v3i.234

Artículo Original

Optimización y validación de modelos computacionales DFT, Ab Initio y G3/G4 para la caracterización físico-química de neurotransmisores en fase gaseosa

Optimization and validation of computational models: DFT, Ab Initio, and G3/G4 for the physicochemical characterization of neurotransmitters in the gas pase

Nancy Mariela, Challapa Velásquez ; José Manuel, Osores Rebaza

Instituto Peruano de Energía Nuclear, San Borja, Perú.

Resumen

La caracterización de la dopamina y su precursor, la L-DOPA, en fase gaseosa constituye un área de investigación con marcada escasez de datos experimentales. Comprender las propiedades físico-químicas intrínsecas de estas especies es esencial, dado su papel central en la neurotransmisión y su implicación directa en patologías neurodegenerativas como la enfermedad de Parkinson. Para abordar esta brecha, se empleó una metodología computacional avanzada que integra la Teoría del Funcional de la Densidad (DFT), métodos Ab Initio y teorías compuestas G3/G4. Esta aproximación permitió determinar con alta precisión la estabilidad termodinámica, la estructura molecular y la reactividad protónica de ambas moléculas. Los cálculos incluyeron un análisis conformacional exhaustivo, orientado a identificar los rotámeros más estables, los cuales fueron optimizados para obtener sus energías electrónicas, entalpías de formación y energías libres de Gibbs. Los resultados revelan que el rotámero G1a representa la conformación más estable de la dopamina neutra, aunque las diferencias energéticas con otros rotámeros como G2 y T son marginales, oscilando entre 2 y 5 kJ/mol según el método empleado. La aplicación de reacciones isodésmicas y de atomización resultó clave para mejorar la exactitud de las entalpías de formación, al mitigar errores sistemáticos inherentes a los cálculos teóricos. En síntesis, este estudio establece un conjunto de datos de referencia de alta calidad, fundamentales para la validación de modelos computacionales futuros y para el avance en la comprensión de la química fundamental de neurotransmisores en condiciones libres de solventes. Este conocimiento no solo fortalece la investigación básica, sino que también ofrece perspectivas prometedoras para el diseño racional de estrategias terapéuticas más eficaces.

Palabras claves: Dopamina, L-DOPA, fase gaseosa, modelos computacionales, reacciones isodésmicas, neurodegenerativas. 

Abstract

The characterization of dopamine and its precursor, L-DOPA, in the gas phase constitutes an area of research with a marked scarcity of experimental data. Understanding the intrinsic physicochemical properties of these species is essential, given their central role in neurotransmission and their direct implication in neurodegenerative pathologies such as Parkinson's disease. To address this gap, an advanced computational methodology was employed, integrating Density Functional Theory (DFT), Ab Initio methods, and composite theories G3/G4. This approach allowed for the high-precision determination of the thermodynamic stability, molecular structure, and proton reactivity of both molecules. The calculations included an exhaustive conformational analysis aimed at identifying the most stable rotamers, which were optimized to obtain their electronic energies, enthalpies of formation, and Gibbs free energies. The results reveal that the G1a rotamer represents the most stable conformation of neutral dopamine. However, the energetic differences with other rotamers like G2 and T are marginal, oscillating between 2 and 5 kJ/mol depending on the method used. The application of isodesmic and atomization reactions proved key to improving the accuracy of the enthalpies of formation by mitigating systematic errors inherent to theoretical calculations. In summary, this study establishes a set of high-quality reference data, fundamental for the validation of future computational models and for advancing the understanding of the fundamental chemistry of neurotransmitters in solvent-free conditions. This knowledge not only strengthens basic research but also offers promising perspectives for the rational design of more effective therapeutic strategies.

Keywords: Dopamine, L-DOPA, gas phase, computational models, isodesmic reactions, neurodegenerative.

Recibido/Received

24-05-2025

Aprobado/Approved

18-08-2025

Publicado/Published

19-08-2025

Introducción

La comprensión de los procesos biológicos a nivel molecular es fundamental para dilucidar los mecanismos de acción de biomoléculas esenciales, como los neurotransmisores. Estas sustancias químicas desempeñan un papel crítico en la comunicación neuronal dentro del sistema nervioso central, regulando una vasta gama de funciones fisiológicas y cognitivas. Entre los neurotransmisores más prominentes y extensamente estudiados se encuentran la dopamina y su precursor, la L-DOPA. Ambos compuestos son pilares en la neuroquímica debido a su implicación en vías dopaminérgicas cruciales, las cuales son responsables del control motor, la motivación, la recompensa y diversas funciones ejecutivas. Sus propiedades físico-químicas inherentes, incluyendo su estabilidad termodinámica, estructura intrínseca y reactividad química, son determinantes para su función biológica y sus interacciones con los receptores y las enzimas (Katritzky et al., 2008; Rajnák et al., 2024).

A pesar de su trascendental importancia, existe una notable escasez de información experimental detallada sobre las propiedades físico-químicas de la dopamina y la L-DOPA en su estado intrínseco, es decir, en fase gaseosa. Esta laguna en el conocimiento se atribuye, en gran medida, a las considerables dificultades técnicas inherentes al aislamiento y estudio de estas biomoléculas fuera de su entorno biológico natural. El medio fisiológico es intrínsecamente complejo, caracterizado por su alta polaridad y la presencia de una miríada de otras moléculas, iones y proteínas, que pueden enmascarar o alterar las propiedades intrínsecas del ligando. El estudio en fase gaseosa ofrece una oportunidad única para desentrañar las características fundamentales de una molécula, liberándola de las influencias del solvente y de las interacciones intermoleculares que dominan en entornos condensados (Abboud et al., 2002; Abboud, 2003). Por lo tanto, la investigación en fase gaseosa se convierte en un punto de referencia ideal para la validación y optimización de modelos computacionales, permitiendo una comprensión más profunda de la química fundamental de estas biomoléculas.

La dopamina, una catecolamina bien conocida, actúa como un neurotransmisor crucial en múltiples circuitos neuronales. Su mecanismo de acción se inicia con su unión a receptores específicos, como los adrenoreceptores, que son hebras de proteínas acopladas a proteínas G (GPCRs). Esta interacción ligando-receptor es altamente específica y se facilita mediante la formación de puentes de hidrógeno entre los grupos hidroxilo (-OH) de la dopamina y los residuos de aminoácidos del sitio activo del receptor (Schulze & Cafiero, 2024). Aunque la importancia de los grupos hidroxilo en esta interacción es indiscutible para la activación del receptor y la transducción de la señal, la contribución de estos mismos grupos a la estabilidad intramolecular de la dopamina, y cómo esta estabilidad puede influir en la afinidad y especificidad de unión al receptor, ha sido una faceta insuficientemente explorada. Comprender estas contribuciones intrínsecas es vital, ya que la conformación y estabilidad de la dopamina antes de la unión pueden dictar su capacidad de acoplamiento y la eficacia de la señalización (Harle et al., 2023).

En entornos fisiológicos, particularmente en disolución acuosa a pH 7.4, la dopamina, al igual que muchos otros neurotransmisores, se encuentra predominantemente en su forma protonada, superando el 92% de la población total de especies. El remanente existe en forma de "zwitterion" o especie neutra (Nagy & Alagona, 2003). Es esta forma protonada la que adquiere mayor relevancia en el enlazamiento con el receptor adrenérgico, siendo este estado de protonación preservado y estabilizado dentro del complejo ligando-receptor activado. Investigaciones previas han corroborado que en disoluciones con pH inferior a 8, la dopamina sufre protonación en su grupo amino terminal (Solmajer et al., 1983). Este comportamiento de protonación es un factor crítico que modula la actividad biológica y la biodisponibilidad de la dopamina, y su estudio detallado en un entorno libre de solvente puede revelar aspectos intrínsecos de su comportamiento ácido-base.

La L-DOPA (L-3,4-dihidroxifenilalanina), por su parte, es una molécula de singular importancia no solo como precursor directo de la dopamina, sino también de otros neurotransmisores fundamentales como la adrenalina y la noradrenalina (Du et al., 2022; de Oliveira et al., 2025). Su aplicación más reconocida en la práctica clínica es como una pro-droga para elevar los niveles de dopamina cerebral en el tratamiento de la enfermedad de Parkinson (Dauer & Przedborski, 2003). Su capacidad para atravesar la barrera hematoencefálica, a diferencia de la dopamina misma, y su posterior descarboxilación en el cerebro para producir dopamina, la convierte en una herramienta terapéutica indispensable. La eficacia de este proceso terapéutico y la comprensión de sus mecanismos requieren un conocimiento exhaustivo de la estructura electrónica de sus diversas formas, tanto protonadas como desprotonadas (Elroby, 2012). Por tanto, la caracterización intrínseca de L-DOPA es igualmente crucial para dilucidar su metabolismo y su perfil farmacológico.

La justificación primordial de este estudio radica en la imperiosa necesidad de llenar el vacío de conocimiento existente con respecto a las propiedades químico-físicas intrínsecas de la dopamina y la L-DOPA. El conocimiento teórico y experimental de propiedades como la estabilidad termodinámica, la estructura molecular y la reactividad por transferencia protónica de especies bioactivas es fundamental para desvelar y comprender una multiplicidad de sus actividades biológicas (Buglak, 2024; Harle et al., 2023). En este sentido, nuestra investigación sobre las propiedades químico-físicas y la reactividad química intrínseca de la dopamina y su precursor L-DOPA pretende contribuir significativamente a un mejor entendimiento de los diversos procesos en los que estas moléculas intervienen, los cuales, al menos desde la perspectiva de la ciencia básica, no han sido suficientemente explorados en fase gaseosa.

En general, es un hecho aceptado que el estado de protonación de un neurotransmisor, cuando actúa como ligando, desempeña un papel trascendental en sus funciones bioquímicas y en la modulación de sus interacciones con macromoléculas biológicas (Rajnák et al., 2024; Hatstat et al., 2023). Sin embargo, la literatura científica apenas recopila información experimental exhaustiva al respecto, especialmente en condiciones que permitan aislar las propiedades intrínsecas de la molécula. Esta falta de datos experimentales de referencia para las especies en fase gaseosa dificulta la validación rigurosa de los modelos computacionales, que son cada vez más utilizados para predecir el comportamiento de estas moléculas en entornos complejos (Katritzky et al., 2008).

Las especies bioactivas que nos proponemos estudiar son de gran actualidad y constituyen objeto de intensa investigación debido al papel central que desempeñan en numerosos procesos neurológicos. Es relevante señalar que una regulación inadecuada de los niveles de dopamina en el cerebro está directamente asociada con la patogénesis de enfermedades neurodegenerativas graves como el Parkinson y trastornos psiquiátricos complejos como la esquizofrenia (Quintanilla et al., 2005). La L-DOPA, como se ha mencionado, es una pro-droga esencial para incrementar los niveles de dopamina en pacientes con Parkinson, subrayando la relevancia clínica de comprender en profundidad su química. La elucidación de las propiedades intrínsecas de estos compuestos no solo avanza la ciencia fundamental, sino que también puede informar el diseño de nuevas estrategias terapéuticas y el desarrollo de fármacos más específicos y eficaces.

La modelización computacional, empleando métodos de alta precisión como la Teoría del Funcional de la Densidad (DFT), los métodos Ab Initio y las teorías compuestas G3/G4, se ha consolidado como una herramienta indispensable en la química moderna para la caracterización de sistemas moleculares, especialmente cuando los datos experimentales son escasos o difíciles de obtener (van Mourik et al., 2014; Ye et al., 2022). Los métodos DFT son ampliamente aplicables en la química, física y biología, permitiendo la predicción de geometrías moleculares, estructuras electrónicas y propiedades termodinámicas con una eficiencia computacional razonable para sistemas de tamaño considerable (Buglak, 2024; Shokuhi Rad et al., 2021). Su capacidad para describir interacciones ligando-proteína es también de gran interés (Schulze & Cafiero, 2024). Por otro lado, los métodos Ab Initio, basados en primeros principios sin parámetros empíricos, ofrecen una descripción aún más rigurosa de la estructura electrónica, siendo fundamentales para entender la naturaleza de diversas señales espectroscópicas y la reactividad (Babaei Bidmeshki et al., 2021).

Para alcanzar una mayor precisión en las predicciones termoquímicas, particularmente en la determinación de energías de formación y afinidades protónicas en fase gaseosa, las teorías compuestas G3 y G4 son herramientas de vanguardia (Curtiss et al., 1998; Blaudeau et al., 1997). Estas metodologías combinan cálculos de diferentes niveles de teoría y tamaños de base para extrapolar a un límite de alta precisión, proporcionando valores termoquímicos con una exactitud cercana a los datos experimentales más precisos (Curtiss et al., 1999). La aplicación de estas teorías permite la determinación de propiedades críticas como la entalpía de formación estándar en fase gaseosa (Delta_fH0_m(g)), que representa la entalpía del proceso de formación de un mol de compuesto a partir de sus elementos o moléculas en sus estados estándar, a una temperatura de referencia de 298.15 K y una presión de 1 bar (10$^5$ Pa). Esta magnitud termodinámica es un indicador directo de la estabilidad energética intrínseca de la molécula (Abboud et al., 2002).

Además de la estabilidad, la reactividad por transferencia protónica es un aspecto crucial para la función biológica de los neurotransmisores. En el contexto de las reacciones ácido-base, la acidez se define, según Brönsted-Lowry, como la capacidad de una sustancia para ceder protones, mientras que la basicidad se refiere a la capacidad de aceptar dichos protones. La determinación de estas propiedades en fase gaseosa proporciona información invaluable sobre la reactividad intrínseca de la dopamina y la L-DOPA, libre de la influencia de los solventes. Para la validación experimental de estas propiedades, el Método Cinético Extendido de Cooks (EKCM), desarrollado por el Profesor Graham Cooks y su grupo de investigación en la Universidad de Purdue (EE. UU.), es una técnica poderosa que permite la determinación experimental de magnitudes termodinámicas como la afinidad y acidez protónicas en fase gaseosa con alta precisión (Armentrout, 2000). La combinación de cálculos de alta precisión con la validación experimental a través de EKCM representa un enfoque robusto para caracterizar completamente la termodinámica de las reacciones de transferencia protónica.

Un aspecto metodológico fundamental en la aplicación de las teorías compuestas y DFT para la determinación de entalpías de formación y otras propiedades termoquímicas es el uso de reacciones isodésmicas. Una reacción isodésmica es una reacción química (real o hipotética) en la cual el número y el tipo de enlaces químicos de un miembro de la reacción son idénticos a los del otro miembro. Este tipo de reacción es invaluable en química computacional porque permite una significativa cancelación de errores sistemáticos asociados con los métodos de cálculo y los conjuntos de bases, resultando en predicciones de energías de reacción y entalpías de formación considerablemente más precisas (Cuba et al., 2021; Zou et al., 2022). Al utilizar reacciones isodésmicas, es posible estimar con mayor confiabilidad las propiedades termoquímicas de moléculas complejas como la dopamina y la L-DOPA, anclando los cálculos a compuestos de referencia con propiedades bien conocidas.

Se propone un enfoque teórico-experimental para la caracterización exhaustiva de la dopamina y la L-DOPA en fase gaseosa. Mediante la aplicación de modelos computacionales de vanguardia como DFT, Ab Initio y G3/G4, se busca determinar la estabilidad termodinámica intrínseca y la reactividad por transferencia protónica de estos neurotransmisores y su precursor. Los resultados de este estudio no solo contribuirán a una comprensión fundamental de la química de estas biomoléculas, sino que también establecerán un conjunto de datos de referencia cruciales para el desarrollo y la validación de modelos computacionales más precisos, que a su vez pueden ser aplicados a sistemas biológicos más complejos, incluyendo interacciones en fase condensada. Además, la sinergia entre capacidades teóricas y experimentales es esencial para avanzar en el conocimiento de las propiedades intrínsecas de biomoléculas de tan alta relevancia como la dopamina y la L-DOPA.

Materiales y métodos

La metodología para la caracterización físico-química de neurotransmisores en fase gaseosa se fundamentó en la química computacional, usando diferentes métodos, incluidos en paquetes de programas como Spartan (implementado en PCs convencionales), Gaussian’03 y Gaussian’09 (Frisch, 2003) implementados en los Clústers LADON-HIDRA (del IQFR-CSIC, Madrid) y TRUENO (CSIC, Madrid).

La secuencia de los cálculos realizados fueron:

· Optimizaciones previas mediante métodos semi-empíricos. Una primera aproximación a la estructura de las moléculas se realizó para todos los sistemas estudiados mediante el método PM3, utilizando el programa Spartan.

· Métodos ab initio. Utilizamos las metodologías G3 y G4

· Métodos DFT. Utilizados tanto para la optimización de estructuras como para la determinación de las frecuencias vibracionales. Se utilizaron métodos B3LYP con bases 631++G(d,p) y 6-311++G(3df,2p).

Es importante mencionar que el cluster LADON consiste en 48 nodos de 64 bits (dual, quad, de máquinas de 6 y 8 núcleos) con 400Gb de RAM y 540 núcleos, interconectados con ethernet Gigabit, Myirinet 2000 y Infiniband. El cluster TRUENO, es un cluster híbrido de arquitecturas x86_64 e ia64 situado en el Campus del CSIC de Madrid. Compuesto por los CPD's de Pinar 19 (SGAI), Serrano 142 (SGAI) y Serrano 121 (Óptica), con un total de 190 nodos,1400cores y una potencia de cálculo, aproximada, de 20 TFlops.

Fundamentos de los modelos computacionales

La Teoría del Funcional de la Densidad (DFT), es un método de la química cuántica que se distingue por su eficiencia computacional, que utiliza la densidad electrónica del sistema como variable fundamental. Y El Métodos Ab Initio, para el cálculo de la solución de la ecuación de Schrödinger, utilizan una serie de aproximaciones matemáticas rigurosas, están basados solamente en las leyes de la mecánica cuántica y en los valores de un pequeño número de constantes físicas. Los métodos ab initio ampliamente usados en modelización molecular son HF (Hartree-Fock). Dentro de esta categoría, se emplearon los métodos de alta precisión Gaussian-3 (G3) y Gaussian-4 (G4), reconocidos por su capacidad para generar resultados termoquímicos de alta exactitud.

Detalles de los cálculos computacionales

Se llevó a cabo un exhaustivo análisis conformacional para la dopamina, dopamina protonada y la L-DOPA. Este análisis consistió en la generación de múltiples rotámeros para cada molécula mediante la rotación de sus ángulos diedros clave. Para la dopamina y su forma protonada, se rotaron los ángulos diedros ϕ 1 (∠C1CβCαN) y ϕ 2 (∠C2C1CβCα), así como los de los grupos OH aromáticos, ϕ 3 (∠C6C5OH) y ϕ 4 (∠C5C4OH). En el caso de la L-DOPA, se incluyó la rotación del grupo ácido carboxílico, descrito por el ángulo diedro ω (∠CβCαC=O).

Los cálculos se realizaron utilizando el funcional híbrido B3LYP y la base de orbitales 6-311++G(d,p) para la optimización inicial de la geometría y el cálculo de frecuencias vibracionales. Los conformeros de mínima energía, identificados como los rotámeros más estables, fueron optimizados en los niveles de teoría G3 y G4 para obtener valores de alta precisión de sus energías totales (E 0), entalpías (H 298) y energías de Gibbs (G 298) a una temperatura de 298,15 K. Estos datos permitieron el cálculo de las entalpías relativas (ΔH) y las poblaciones conformacionales, utilizando la ecuación de equilibrio (14) para determinar la abundancia de cada rotámero.

El análisis conformacional de la dopamina y L-DOPA se hizo usando el programa SPARTAN (al nivel semi-empírico PM3) obteniéndose 100 confórmeros (rotámeros), de los cuales se hicieron una criba hasta obtener alrededor de una decena de ellos, aplicando el criterio de considerar rotámeros cuya diferencia con el más estable es menor de 15 kJ/mol; dado que la contribución a la población conformacional de los que superan esta diferencia son menos del 1% del total. Las geometrías de los rotámeros más significativos se optimizaron en una etapa siguiente con el Programa Gaussian 03 (Clúster LADON) al nivel B3LYP/3-21G(d). Finalmente, y usando el programa Gaussian 09, tanto en el clúster LADON como en TRUENO, todos las geometrías de los rotámeros considerados se optimizaron, incluyendo la determinación de frecuencias vibracionales, a los niveles B3LYP/6-311++G(d,p) [y también 6-311++G(3df,2p)], G3 y G4.

Se aplicaron reacciones isodésmicas y de atomización para refinar los valores termoquímicos, como las entalpías de formación.

Reacciones isodésmicas

Las reacciones isodésmicas, en las que el número y tipo de enlaces se mantienen constantes en reactivos y productos, permiten una cancelación de errores sistemáticos inherentes a las aproximaciones computacionales, lo que se traduce en entalpías de formación más exactas. Estos métodos se emplearon para validar y corregir los valores obtenidos por los métodos de Gaussian, proporcionando una base sólida para la caracterización de los neurotransmisores.

Son reacciones químicas (reales o hipotéticas) en el cual el número y tipo de enlaces químicos de un miembro es el mismo que el del otro. Los enlaces químicos rotos en los reactivos son los mismos que los enlaces formados en los productos.

Por ejemplo, la siguiente reacción es una isodésmica:

BSI (“Bond separation Isodesmic reactions”): es una sub-clase de reacciones isodésmicas que incluye moléculas sencillas con enlaces representativos, p.ejem CH₃−CH₃, CH₂=CH₂, CH≡CH, CH₃−OH, CH₃−O−CH₃, CH₃−NH2, CH₃−NH−CH₃, etc. Estas especies se tienen en cuenta a la hora de configurar la reacción isodésmica que involucra la especie de interés.

El balance de enlaces y átomos tanto en reactantes como en productos de una reacción isodésmica permite la compensación de factores termodinámicos en ambos miembros. Para la obtención de la entalpía de formación, Δ_fH⁰_m(g), de una determinada especie se combinan valores experimentales del resto de compuestos (considerados como referencias) y la entalpía de la reacción calculada habitualmente mediante métodos computacionales.

Reacción de atomización

Descompone una molécula en sus átomos constituyentes en estado gaseoso, permitiendo calcular su entalpía de formación a partir de las energías de disociación; para expresar en términos de las energías de los constituyentes atómicos y por otra, en términos de entalpías de formación experimentales de los mismos, todos a 0K. De esta manera se deduce la entalpía formación de la especie en cuestión a 0K, Δ_fH⁰_m(g,0K). Finalmente, la entalpía de formación estándar a 298.15K, Δ_fH⁰_m(g), se determina considerando capacidades caloríficas tanto calculadas como experimentales de la especie en cuestión y de sus constituyentes moleculares en su expresión más sencilla.

Resultados

Análisis conformacional

En la Figura 1 sección “a”, se muestra el esquema conformacional de la dopamina y su precursor L-DOPA, generados por rotaciones de los grupos aromático, NH₂, OH o COOH (en caso de la L-DOPA). Tras una considerable cantidad de rotámeros, varios de ellos con estructuras enantioméricas, generados principalmente por rotaciones alrededor de los enlaces C−N y C−C. Ahora bien, esta variabilidad conformacional, es definida por los ángulos diedros φ_n (n=1,2,3,4), así φ₁ (∠C₁C_βC_αN) describe la rotación del grupo metil-amino; φ₂ (∠C₂C₁C_βC_α) la rotación del grupo aromático difenólico (catecol); φ₃ (∠C₆C₅OH) y φ₄ (∠C₅C₄OH) rotación de los OH del grupo aromático. En el caso de la L-DOPA la rotación de su grupo ácido viene descrito por el ángulo diedro ω (∠C_βC_αC=O).

Dado que los cálculos computacionales incluyen la determinación de frecuencias; éstos permiten obtener magnitudes termodinámicas moleculares entalpías H, entropías S y energías de Gibbs G a la temperatura de referencia 298,15 K (25 ^oC). La población de los rotámeros estables considerados se obtiene a partir de la reacción de equilibrio (1) entre el rotámero más estable (A) y cualquier otro, B:

Figura 1. Análisis conformacional dopamina y su precursor L-DOPA

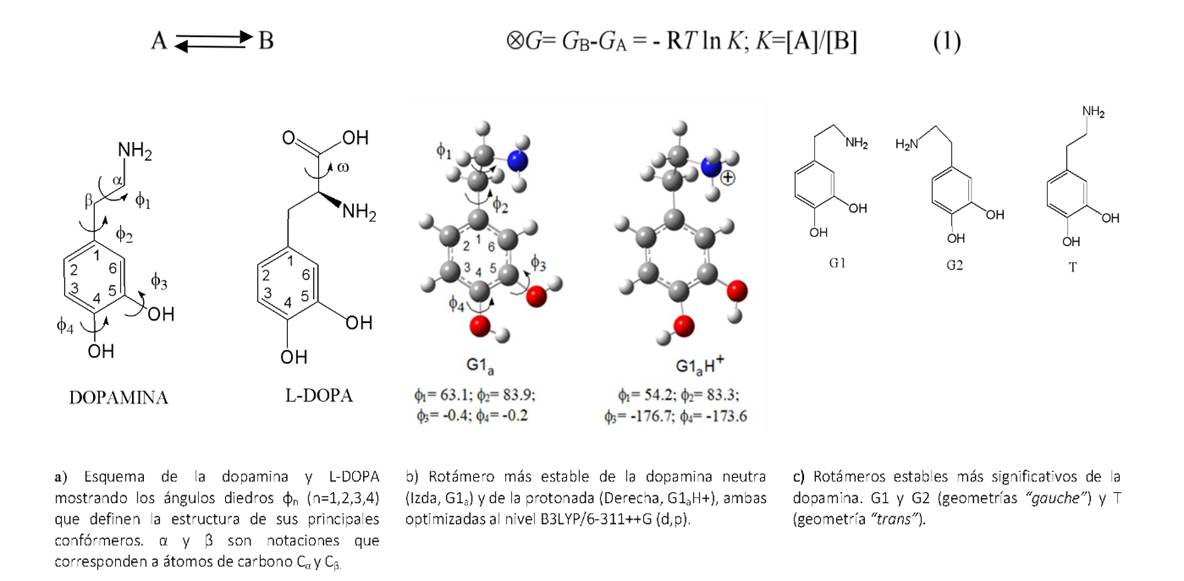
Rotámeros de la dopamina neutra

Los rotámeros más estables de la dopamina están caracterizados por incluir el grupo aromático plano con puente de hidrógeno (O∙∙∙H∙∙∙O) formado por sus grupos OH. Los podemos agrupar en 3 tipos: G1 y G2 son geometrías “gauche” caracterizados por el grupo amino situado en un plano casi-perpendicular y próximo al grupo aromático difenólico (9b). Y los T que son geometrías “trans” con el grupo NH₂ alejado del aromático (Figura 9c). En la Tabla 1 se muestran los parámetros energéticos de las geometrías estables más significativas de la dopamina, obtenidos tanto a niveles DFT (B3LYP/6-311++G(d,p)) como ab initio (G3 y G4).

Como podemos apreciar, G1_a es tan solo 2 kJ/mol más estable que los rotámeros del tipo G2 y T si tenemos en cuenta cálculos B3LYP/6-311++G (d,p); en cambio esta diferencia aumenta ligeramente a menos de 5 kJ/mol para cálculos G3 y G4.  

Rotámeros de la dopamina protonada

Usando la misma notación de geometría molecular de la dopanima neutra, para la protona en el nitrógeno de su grupo NH₂ (Figura 9b). Se evidenció que los rotámeros más significativos son del tipo “gauche” y los podemos agrupar según la orientación del grupo NH₃⁺ a uno (+φ₁) u otro lado (-φ₁) del plano perpendicular al grupo aromático difenólico. Mientras que las dopaminas protonadas del tipo “trans” son al menos 18 kJ/mol menos estable que G1_aH⁺. Los rotámeros más estables, G1_aH⁺ y G2_aH⁺ representan más del 86% de la población conformacional considerada. En la Tabla 2 se muestran los parámetros energéticos de las geometrías estables más significativas de la dopamina protonada, obtenidos al nivel B3LYP/6-311++G(d,p).

Rotámeros de la L-DOPA neutra

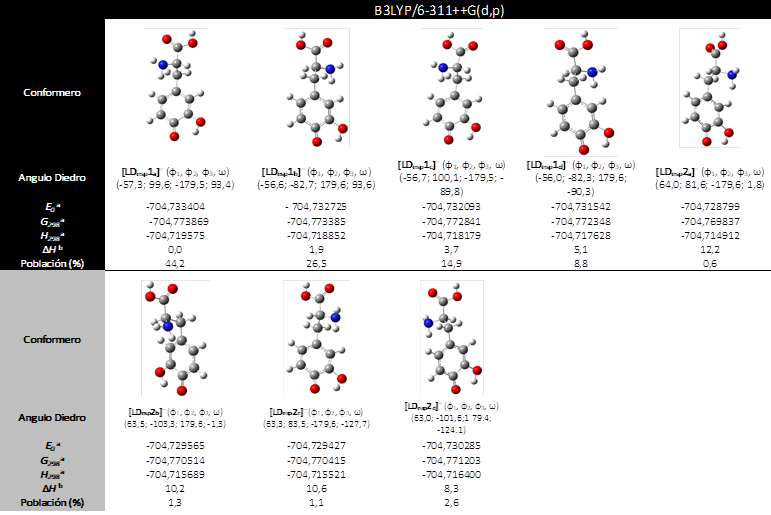
Al igual que en el caso de la dopamina, los rotámeros más estables de la L-DOPA están caracterizados por el grupo aromático difenólico plano con puente de hidrógeno (O∙∙∙H∙∙∙O) formado por sus grupos OH. Los rotámeros más significativos presentan al grupo amino casi en un plano perpendicular al aromático, similar a los rotámeros “gauche” de la dopamina (Figura 2). Los podemos agrupar según la orientación del grupo amino a uno (-φ₁) u otro lado (+φ₁) del plano perpendicular al grupo aromático, LD1_x y LD2_x (x=a,b,…h), respectivamente. El rotámero más estable LD1_a es al menos 5.3 y 3.6 kJ/mol más estable que el resto de rotámeros LD1_x y LD2_x, respectivamente; tanto al nivel de cálculo B3LYP/6-311++G(d,p) como al G3. Estos resultados muestran también una relativa uniformidad en la distribución conformacional de la L-DOPA. Es importante mencionar que la población del 1er grupo llega a ser casi un 56% de la población total.

Tabla 1. Resultados computacionales para la dopamina neutra, obtenidas a los niveles de teoría B3LYP, G3 y G4

En la 1era columna se describen los ángulos diedros para cada rotámero. Las entalpías relativas ΔH se determinan respecto del rotámero más estable.

^a Todos los valores en unidades de Hartree/partícula. ^b Valores expresados en kJ/mol. E₀ = Energía total a 0 K. H₂₉₈= Entalpías y G₂₉₈ = energías de Gibbs a 298,15 K.

En la Tabla 3 se muestran los parámetros energéticos de las geometrías estables más significativas de la L-DOPA, obtenidos tanto a niveles B3LYP/6-311++G(d,p) como a G3. El tamaño de la molécula ha sido uno de los limitantes que nos impidió realizar cálculos al nivel G4.

Tabla 2. Resultados computacionales para la dopamina protonada, obtenidas al nivel B3LYP/6-311++G(d,p)

En la 1era columna se describen los ángulos diedros para cada rotámero. Las entalpías relativas ΔH se determinan respecto del rotámero más estable.

^a Todos los valores en unidades de Hartree/partícula. ^b Valores expresados en kJ/mol. E₀ = Energía total a 0 K. H₂₉₈= Entalpías y G₂₉₈ = energías de Gibbs a 298,15 K.

Figura 2.  Rotámero más estable de la L-DOPA neutra (Izqda. LD1_a) y de la desprotonada (Derecha, [LD_esp1_a]⁻ ), ambas optimizadas al nivel B3LYP/6-311++G(d,p)

Tabla 3. Resultados computacionales para la L-DOPA neutra, obtenidas a los niveles de teoría B3LYP, y G3

En la 1era columna se describen los ángulos diedros para cada rotámero. Las entalpías relativas ΔH se determinan respecto del rotámero más estable [LD_esp1_a]⁻. ^a Todos los valores en unidades de Hartree/partícula. ^b Valores expresados en kJ/mol. E₀ = Energía total a 0 K. H₂₉₈= Entalpías y G₂₉₈ = energías de Gibbs a 298,15 K

Rotámeros de la L-DOPA desprotonada

La L-DOPA se desprotona preferentemente en el OH asociado al C(4) del grupo aromático difenólico (Figura 2). La notación usada para la geometría molecular de los aniones L-DOPA desprotonados, [LD_esp1_x]⁻, es la misma que para la neutra. Los rotámeros más significativos son similares a los correspondientes neutros LD1, siendo [LD_esp1_a]⁻ hasta 5.1 kJ/mol más estable que los demás, con una abundancia de casi 44% (Tabla 4). El grupo de aniones desprotonados con estructura similar a LD2, [LD_esp2_x]⁻ son hasta 12.2 kJ/mol menos estable que [LD_esp1_a]⁻ y representan menos del 6% de la población conformacional.

Es importante mencionar que [LD_esp1_a]⁻ es 5.6 y 7.8 kJ/mol más estable que los rotámeros más significativos desprotonados en el OH del C(5) y en el grupo COOH, respectivamente. Este resultado justifica la desprotonación preferente en C(4)OH antes descrita

Tabla 4.  Resultados computacionales para la L-DOPA desprotonada, [LD_esp1_x]⁻, obtenidas al nivel de teoría B3LYP/6-311++G(d,p)

En la 1era columna se describen los ángulos diedros para cada rotámero. Las entalpías relativas ΔH se determinan respecto del rotámero más estable [LD_esp1_a]⁻.

^a Todos los valores en unidades de Hartree/partícula. ^b Valores expresados en kJ/mol. E₀ = Energía total a 0 K. H₂₉₈= Entalpías y G₂₉₈ = energías de Gibbs a 298,15 K

Estabilidad termodinámica intrínseca: Determinación de la entalpía de formación en fase gaseosa ( D_fH⁰_m(g)) de la dopamina y la L-DOPA

Los valores de entalpías estándar de reacción y de formación obtenidos mediante metodologías de atomización y reacciones isodésmicas, aplicadas tanto a la dopamina como a su precursor, la L-DOPA. La reacción (2), correspondiente a la dopamina (C₈H₁₁NO₂), es una isodésmica del tipo BSI. Su entalpía de reacción (D_rH⁰_m (2)) fue determinada computacionalmente al nivel B3LYP/6-311++G(3df,2p), mientras que las entalpías de las demás reacciones isodésmicas se calcularon al nivel B3LYP/6-311++G(d,p).

Las ecuaciones isodésmicas utilizadas fueron las siguientes:

C₈H₁₁NO₂ + 11CH₄ → 3CH₂=CH₂ + 5CH₃CH₃ + 2CH₃OH + CH₃NH₂  (2)

Para los compuestos de referencia, se utilizaron los siguientes valores experimentales de entalpía de formación en fase gaseosa (kJ/mol): metano (-74.87 ± 0.34), etano (-84.0 ± 0.4), eteno (52.47 ± 0.30), fenol (-96.36 ± 0.59), catecol (-274.8 ± 1.2) del NIST; metanol (-201.5 ± 0.2), metilamina (-23.4 ± 1), etilamina (-47.5 ± 0.6), propilamina (-69.9 ± 0.8) de la base de datos de Pedley.

Para la L-DOPA (C₉H₁₁NO₄), la reacción (3) también es isodésmica del tipo BSI y su entalpía de reacción se determinó al nivel B3LYP/6-311++G(3df,2p). La reacción (4) se calculó al nivel B3LYP/6-311++G(d,p):

C₉H₁₁NO₄ + 14CH₄ → 3CH₂=CH₂ + 6CH₃CH₃ + 3CH₃OH + CH₃NH₂ + H₂C=O (3)

C₉H₁₁NO₄ + 4CH₄ → NH₂CH₂COOH + C₆H₅OH + CH₃OH + CH₃CH₂CH₃ (4)

Los valores experimentales de referencia (kJ/mol) fueron tomados del NIST: formaldehído (-115.9 ± 0.5), glicina (-390.5 ± 4.6) y propano (-104.7 ± 0.5).

Afinidad protónica y acidez de la dopamina y la L-DOPA

La afinidad protónica (PA) y la basicidad (GB) de la dopamina, así como la acidez (GA) y la entalpía de acidez (∆_acidH⁰) de la L-DOPA, fueron determinadas mediante cálculos computacionales basados en reacciones de protonación y desprotonación en fase gaseosa. Los cálculos se realizaron al nivel B3LYP/6-311++G(d,p), considerando promedios ponderados de las entalpías H₂₉₈ y energías de Gibbs G₂₉₈ de las conformaciones neutras y sus especies protonadas o desprotonadas.

Para el protón (H⁺), se utilizaron los valores H₂₉₈ = 6.1975 kJ/mol y G₂₉₈ = -0.01 Ha. Las entropías de protonación y desprotonación se calcularon mediante la relación H = G + TS, con T = 298.15 K. Los resultados obtenidos para la dopamina fueron: PA = 942.7 kJ/mol, GB = 905.6 kJ/mol y una entropía de protonación ΔpS⁰ = 124.4 J/mol·K. Para la L-DOPA, se obtuvo una entalpía de acidez ∆_acidH⁰ = 1385.3 kJ/mol, una acidez GA = 1357.7 kJ/mol y una entropía de desprotonación Δ_acidS⁰ = 90.3 J/mol·K.

Discusión

Caracterización físico-química de neurotransmisores en fase gaseosa

Partiendo de que “La comprensión de las propiedades intrínsecas de las biomoléculas es esencial para dilucidar sus mecanismos de acción en complejos sistemas biológicos”. Este estudio abordó la caracterización físico-química de neurotransmisores clave como la dopamina y su precursor L-DOPA en fase gaseosa, empleando una combinación de métodos computacionales de alta precisión como la Teoría del Funcional de la Densidad (DFT), Ab Initio y teorías compuestas G3/G4. La fase gaseosa, al eliminar las influencias del solvente y las interacciones intermoleculares, proporciona un entorno ideal para desentrañar las características fundamentales de una molécula, sirviendo como un punto de referencia crucial para la validación de modelos computacionales (Abboud et al., 2002; Abboud, 2003). Se demostró la estabilidad conformacional, las entalpías de formación y la reactividad protónica de estas especies, aspectos que son fundamentales para entender su función biológica y su implicación en procesos neurológicos.

Análisis conformacional y estructura intrínseca

El análisis conformacional es un paso inicial y fundamental para comprender el comportamiento de moléculas flexibles como la dopamina y la L-DOPA. Nuestros resultados muestran una compleja superficie de energía potencial para ambas moléculas, caracterizada por la existencia de múltiples rotámeros estables. Para la dopamina neutra, se identificaron tres tipos principales de conformaciones: gauche (G1 y G2) y trans (T). El rotámero G1a se reveló como el más estable, aunque con diferencias energéticas mínimas (inferiores a 5 kJ/mol) respecto a los rotámeros G2 y T, especialmente con los cálculos G3 y G4 de mayor nivel de teoría. Además. la presencia de un puente de hidrógeno intramolecular entre los grupos hidroxilo del grupo aromático difenólico en los rotámeros más estables de la dopamina neutra es consistente con estudios previos que resaltan la importancia de estas interacciones para la estabilidad molecular (Rajnák et al., 2024). La relativa cercanía energética entre los diversos conformeros subraya la flexibilidad conformacional de la dopamina, lo cual podría ser relevante para su capacidad de interacción con diferentes receptores o enzimas en el entorno biológico (Katritzky et al., 2008).

En el caso de la dopamina protonada (en el grupo amino), las conformaciones gauche (G1aH$^+$ y G2aH$^+$) predominan significativamente, representando más del 86% de la población conformacional total; mientras que las conformaciones trans fueron al menos 18 kJ/mol menos estable. Esta clara preferencia por las geometrías gauche en la dopamina protonada sugiere una fuerte influencia del grupo amino protonado en la conformación más estable, posiblemente debido a interacciones electrostáticas o puentes de hidrógeno intramoleculares estabilizadores con el resto de la molécula. Esta diferencia conformacional entre la dopamina neutra y protonada es crucial, ya que en el entorno fisiológico (pH 7.4), la dopamina existe predominantemente en su forma protonada (Nagy & Alagona, 2003; Solmajer et al., 1983). Por lo tanto, comprender la estructura intrínseca de la forma protonada es vital para predecir su interacción con los receptores adrenérgicos (Schulze & Cafiero, 2024).

Para la L-DOPA neutra, los rotámeros más estables también se caracterizaron por el grupo aromático difenólico plano con un puente de hidrógeno intramolecular. De manera similar a la dopamina, los conformeros con el grupo amino en un plano casi perpendicular al aromático (tipos LD1 y LD2) fueron los más significativos. El rotámero LD1a mostró ser el más estable, con una diferencia de energía de al menos 3.6 kJ/mol respecto a otros conformeros LD2x, y su grupo representó casi el 56% de la población total. La similitud en los patrones conformacionales entre la dopamina y la L-DOPA neutras es esperable, dada su relación estructural directa. Es importante señalar que, debido al mayor tamaño de la L-DOPA, no fue posible realizar cálculos al nivel G4, lo cual resalta las limitaciones computacionales que aún persisten para moléculas biomoleculares más grandes, a pesar de la potencia de los clústeres utilizados.

Finalmente, el análisis de la L-DOPA desprotonada reveló una clara preferencia por la desprotonación en el grupo hidroxilo del C(4) del anillo aromático difenólico. Los rotámeros desprotonados de tipo [LDesp1x]− (similares a los neutros LD1) fueron los más estables, con [LDesp1a]− siendo hasta 5.1 kJ/mol más estable que otros conformeros y representando una abundancia de casi el 44%. Las especies desprotonadas en el C(5)OH o en el grupo carboxilo fueron significativamente menos estables (5.6 y 7.8 kJ/mol, respectivamente). Esta selectividad en la desprotonación es un hallazgo clave, ya que la forma aniónica de la L-DOPA juega un papel en su metabolismo y en su interacción con enzimas (Elroby, 2012; Du et al., 2022). La caracterización de estas estructuras intrínsecas proporciona una base fundamental para comprender su reactividad y actividad biológica.

Estabilidad Termodinámica Intrínseca: Entalpía de Formación en Fase Gaseosa (ΔfHm0(g))

La determinación precisa de la entalpía de formación en fase gaseosa (ΔfHm0(g)) es un indicador directo de la estabilidad energética intrínseca de una molécula y es crucial para el modelado termoquímico. En este estudio, se emplearon tanto metodologías de atomización como reacciones isodésmicas para calcular esta propiedad para la dopamina y la L-DOPA. El uso de reacciones isodésmicas, particularmente del tipo BSI (Bond Separation Isodesmic reactions), es una estrategia computacionalmente robusta que permite una significativa cancelación de errores sistemáticos asociados con las aproximaciones de los métodos de cálculo y los conjuntos de bases (Cuba et al., 2021; Zou et al., 2022). En predicciones de entalpías de reacción y entalpías de formación considerablemente más precisas, anclando los cálculos a compuestos de referencia con propiedades termoquímicas bien conocidas experimentalmente.

La aplicación de la reacción isodésmica tipo BSI para la dopamina y la L-DOPA, combinada con valores experimentales de referencia para los compuestos modelo, asegura que los valores de ΔfHm0(g) obtenidos sean de alta fiabilidad. Estos valores intrínsecos de estabilidad son de gran utilidad para comparar la estabilidad relativa de los diferentes conformeros en fase gaseosa y para establecer una línea base que pueda ser utilizada en estudios futuros sobre la termodinámica de las interacciones de estas moléculas en entornos más complejos, como soluciones acuosas o sitios activos de enzimas. La importancia de la estabilidad termodinámica intrínseca ha sido destacada en otros estudios de moléculas biológicamente relevantes (Abboud et al., 2002).

Afinidad protónica y acidez en fase gaseosa

La reactividad por transferencia protónica es un aspecto crucial que gobierna la función biológica de los neurotransmisores. La determinación de la Afinidad Protónica (PA) y la Basiscidad Gaseosa (GB) para la dopamina, y la Acidez Gaseosa (GA) y la Entalpía de Acidez (ΔacidH0) para la L-DOPA en fase gaseosa, proporciona información invaluable sobre su comportamiento ácido-base intrínseco, libre de las complejidades de la solvatación.

Para la dopamina, se calculó una afinidad protónica (PA) de 942.7 kJ/mol y una basicidad gaseosa (GB) de 905.6 kJ/mol. Estos valores reflejan la capacidad intrínseca de la dopamina para aceptar un protón, lo cual es predominantemente en su grupo amino terminal. Este comportamiento de protonación es un factor crítico que modula la actividad biológica y la biodisponibilidad de la dopamina, ya que su estado de protonación en disolución acuosa a pH fisiológico (7.4) es mayoritariamente protonado (Nagy & Alagona, 2003; Solmajer et al., 1983). Los resultados en fase gaseosa proporcionan una referencia fundamental para entender cómo estas propiedades intrínsecas se ven moduladas por el entorno. La entropía de protonación ΔpS0 de 124.4 J/mol·K indica los cambios en el desorden molecular asociados con el proceso de protonación en fase gaseosa, que son importantes para una descripción termodinámica completa (Armentrout, 2000).

Para la L-DOPA, se obtuvo una entalpía de acidez (ΔacidH0) de 1385.3 kJ/mol y una acidez gaseosa (GA) de 1357.7 kJ/mol, con una entropía de desprotonación (ΔacidS0) de 90.3 J/mol·K. El hecho de que la L-DOPA se desprotone preferentemente en el OH asociado al C(4) del grupo aromático difenólico es un hallazgo de particular interés, corroborando su comportamiento intrínseco revelado por el análisis conformacional de las especies desprotonadas. Esta información es crucial, ya que las propiedades ácido-base de la L-DOPA influyen en su metabolismo y en su capacidad para actuar como precursor de la dopamina y otros neurotransmisores (Elroby, 2012; Du et al., 2022). La reactividad protónica en fase gaseosa sirve como un punto de partida termodinámico para comprender su comportamiento en entornos biológicos complejos, donde la solvatación y las interacciones con proteínas modulan significativamente estas propiedades (Rajnák et al., 2024; Hatstat et al., 2023).

Consideraciones metodológicas e implicaciones

La elección y aplicación de métodos computacionales de alta precisión como DFT, Ab Initio y las teorías compuestas G3/G4 fueron cruciales para la robustez de este estudio. Los métodos DFT son ampliamente reconocidos por su eficiencia y aplicabilidad en una vasta gama de sistemas moleculares, permitiendo la predicción de geometrías moleculares, estructuras electrónicas y propiedades termodinámicas (van Mourik et al., 2014; Buglak, 2024; Shokuhi Rad et al., 2021). Su capacidad para describir interacciones ligando-proteína también los hace valiosos para futuras extensiones (Schulze & Cafiero, 2024). Los métodos Ab Initio, al basarse en primeros principios, ofrecen una descripción rigurosa de la estructura electrónica, fundamental para entender fenómenos espectroscópicos y reactividad (Babaei Bidmeshki et al., 2021).

Las teorías compuestas G3 y G4 son herramientas de vanguardia para la predicción termoquímica, combinando cálculos de diferentes niveles de teoría y tamaños de base para extrapolar a un límite de alta precisión (Curtiss et al., 1998; Blaudeau et al., 1997). Aunque no fue posible aplicar G4 a la L-DOPA debido a su tamaño molecular y las exigencias computacionales, la consistencia observada entre los resultados de B3LYP y G3 para la dopamina y L-DOPA neutra refuerza la fiabilidad de las predicciones obtenidas. La implementación de estos cálculos en clústeres de alto rendimiento como LADON-HIDRA y TRUENO fue indispensable para manejar la complejidad computacional de las biomoléculas estudiadas.

La sinergia entre las capacidades teóricas y una potencial validación experimental es esencial. Aunque este estudio se centró en la modelización computacional, la referencia al Método Cinético Extendido de Cooks (EKCM) subraya la importancia de la experimentación para la validación rigurosa de las magnitudes termodinámicas en fase gaseosa, como la afinidad y acidez protónicas (Armentrout, 2000). La colaboración con grupos experimentales que posean instrumentación especializada en espectrometría de masas, como el grupo del Dr. Dávalos del IQFR-CSIC, es fundamental para cerrar la brecha entre la teoría y el experimento y asegurar la fiabilidad de los hallazgos.

Relevancia biológica y perspectivas futuras

La elucidación de las propiedades físico-químicas intrínsecas de la dopamina y la L-DOPA tiene profundas implicaciones para la neurociencia y la farmacología. La dopamina es un neurotransmisor crucial en múltiples circuitos neuronales, involucrada en el control motor, la motivación y la recompensa. Una desregulación de sus niveles está directamente asociada con enfermedades neurodegenerativas como el Parkinson y trastornos psiquiátricos como la esquizofrenia (Quintanilla et al., 2005). La L-DOPA es una pro-droga vital en el tratamiento del Parkinson, capaz de atravesar la barrera hematoencefálica y convertirse en dopamina en el cerebro (Dauer & Przedborski, 2003).

Comprender la estructura conformacional y la reactividad protónica intrínseca de estas moléculas en fase gaseosa proporciona una base fundamental para el diseño racional de nuevos fármacos. Por ejemplo, el conocimiento detallado sobre la preferencia de protonación y desprotonación puede guiar el desarrollo de análogos de la dopamina con perfiles de afinidad y especificidad mejorados hacia sus receptores, así como el diseño de inhibidores de enzimas que modulan su metabolismo, como la catecol-O-metiltransferasa (COMT) (Hatstat et al., 2023). La investigación actual en torno a las interacciones de fármacos con enzimas relevantes en el metabolismo de la dopamina, como la interacción del paracetamol con enzimas involucradas en el metabolismo de la dopamina, subraya la importancia de este tipo de estudios fundamentales (Harle et al., 2023).

Además, los datos obtenidos en este estudio pueden servir como un valioso conjunto de datos de referencia para el desarrollo y la validación de modelos computacionales más complejos que incorporen los efectos del solvente y las interacciones con macromoléculas biológicas en fase condensada (Katritzky et al., 2008). Estos modelos avanzados son esenciales para simular con mayor precisión el comportamiento de los neurotransmisores en su entorno biológico natural. La metodología computacional empleada en este trabajo puede ser extrapolada a otras biomoléculas y sistemas de interés farmacológico, contribuyendo al avance de la química computacional en el descubrimiento y diseño de fármacos (Ye et al., 2022). La continua investigación sobre las propiedades moleculares de las catecolaminas, incluyendo la dopamina y L-DOPA, en diversos entornos, incluso en agua, sigue siendo un área activa de estudio (Rajnák et al., 2024), lo que valida la relevancia de las propiedades intrínsecas determinadas en esta investigación. La contribución de este trabajo radica en ofrecer una base de conocimiento fundamental que, al complementarse con estudios en fase condensada y experimentales, potenciará el desarrollo de estrategias terapéuticas más específicas y eficaces para abordar enfermedades neurológicas.

Consideraciones finales

Queda en evidencia la apremiante necesidad de superar la carencia de datos experimentales sobre las propiedades intrínsecas de la dopamina y su precursor, la L-DOPA, en fase gaseosa. Mediante la implementación de un enfoque metodológico de alta rigurosidad, que integra modelos computacionales avanzados, incluyendo la Teoría del Funcional de la Densidad (DFT), métodos Ab Initio y teorías compuestas G3/G4, se logró caracterizar con precisión la estabilidad termodinámica y la reactividad protónica de estas biomoléculas. Los resultados obtenidos constituyen una contribución sustantiva a la química fundamental de neurotransmisores, al establecer un conjunto de datos de referencia indispensable para la validación y optimización de futuras simulaciones computacionales.

La estrategia metodológica empleada incorporó un análisis conformacional exhaustivo, así como la aplicación de reacciones isodésmicas y de atomización, las cuales demostraron ser herramientas eficaces para la caracterización de sistemas moleculares de alta complejidad. En particular, las reacciones isodésmicas permitieron minimizar errores sistemáticos inherentes a los cálculos teóricos, lo que se tradujo en estimaciones termoquímicas más precisas, como las entalpías de formación. La articulación entre el rigor teórico y la posibilidad de validación experimental, por ejemplo, mediante el Método Cinético Extendido de Cooks (EKCM), confiere robustez a los resultados y abre nuevas vías para el estudio de la termodinámica de biomoléculas en condiciones libres de solventes.

Más allá de su valor en la ciencia básica, los hallazgos de este estudio poseen implicaciones translacionales relevantes. Una comprensión detallada de las propiedades intrínsecas de la dopamina y la L-DOPA, incluyendo su comportamiento ácido-base y su estabilidad molecular, resulta esencial para el diseño racional de estrategias terapéuticas y el desarrollo de agentes farmacológicos más específicos y eficaces. En este sentido, la investigación no solo enriquece el campo de la neuroquímica computacional, sino que también establece las bases para la extrapolación de estos modelos a sistemas biológicos de mayor complejidad, con potencial impacto en el tratamiento de enfermedades neurodegenerativas como el Parkinson y otros trastornos neurológicos.

Agradecimientos

Es importante destacar que la realización de esta investigación ha sido posible gracias a la valiosa colaboración con el grupo del Dr. Dávalos del Instituto de Química Física Rocasolano (IQFR-CSIC) en Madrid, España. Este grupo dispone de una instrumentación única y versátil, incluyendo espectrometría de masas avanzada y clusters de cálculo computacional de alto rendimiento. Esta infraestructura de vanguardia es idónea para abordar con éxito los temas planteados en el desarrollo de esta tesis, permitiendo la complementación de los datos teóricos con validaciones experimentales en fase gaseosa y asegurando la rigurosidad y fiabilidad de los hallazgos.

Conflicto de intereses

No se reporta conflicto de intereses.

Referencias

Abboud, J. (2003). Protonation of cubane in the gas phase: a high-level Ab initio and DFT study. Angewandte Chemie International Edition, 42(9), 1044–1046. https://doi.org/10.1002/anie.200390269

Abboud, J. L., Castaño, O., Dávalos, J. Z., Jiménez, P., Gomperts, R., Müller, P., & Roux, M. V. (2002). Intrinsic (gas phase) thermodynamic stability of 2-adamantyl cation. Its bearing on the solvolysis rates of 2-adamantyl derivatives. The Journal of organic chemistry, 67(4), 1057–1060. https://doi.org/10.1021/jo016206f

Armentrout, P. B. (2000). Entropy measurements and the kinetic method: A statistically meaningful approach. Journal of the American Society for Mass Spectrometry, 11(5), 371–379. https://doi.org/10.1016/S1044-0305(00)00102-1

Babaei Bidmeshki, N., Azar, T., Ziaie, F., & Janbazi, M. (2021). Unravelling the nature of the alpha-keratin EPR signal: an ab initio study. Physical Chemistry Chemical Physics, 23(11), 6815–6822. https://doi.org/10.1039/d0cp05930g

Blaudeau, J. P., McGrath, M. P., Curtiss, L. A., & Radom, L. (1997). Extension of Gaussian-2 (G2) theory to molecules containing third-row atoms K and Ca. The Journal of Chemical Physics, 107(13), 5016–5021. https://doi.org/10.1063/1.474868

Buglak, A. A. (2024). Antioxidant properties of alpha-amino acids: a density functional theory viewpoint. Free Radical Research, 58(6-7), 380–387. https://doi.org/10.1080/10715762.2024.2385338

Cuba, J. P. B., Alves, G. G. B., Galindo, L. A., Paulin, J. V., & Batagin-Neto, A. (2021). Sulfonated melanin derivatives: theoretical evaluation of local reactivities and chemical structures. Journal of Molecular Modeling, 27(12), Article 362. https://doi.org/10.1007/s00894-021-04982-z

Curtiss, L. A., Raghavachari, K., Redfern, P. C., & Pople, J. A. (1999). Investigation of the use of B3LYP zero-point energies and geometries in the calculation of enthalpies of formation. Chemical Physics Letters, 270(4-6), 437–442. https://doi.org/10.1016/S0009-2614(97)00344-3

Curtiss, L. A., Raghavachari, K., Redfern, P. C., Rassolov, V., & Pople, J. A. (1998). Gaussian-3 (G3) theory for molecules containing first and second-row atoms. The Journal of Chemical Physics, 109(18), 7764–7776. https://doi.org/10.1063/1.477422

Dauer, W., & Przedborski, S. (2003). Parkinson's Disease: Mechanisms and Treatments. Neuron, 39(6), 889–909. https://doi.org/10.1016/S0896-6273(03)00561-4

de Oliveira, T. A., Martin, C. S., Rubira, R. J. G., de Barros, A., Mazali, I. O., Zidoi, L. P., Batagin-Neto, A., & Constantino, C. J. L. (2025). Gold Nanorod Surface-Enhanced Raman Spectroscopy Substrate for l-DOPA Detection: Experimental and Theoretical Approaches. Applied Spectroscopy, 79(7), 1091–1101. https://doi.org/10.1177/00037028251315208

Du, D., Su, Y., Shang, Q., Chen, C., Tang, W., Zhang, L., Ren, H., & Liu, W. (2022). Biomimetic synthesis of L-DOPA inspired by tyrosine hydroxylase. Journal of Inorganic Biochemistry, 234, Article 111878. https://doi.org/10.1016/j.jinorgbio.2022.111878

Elroby, S. A. K. (2012). Understanding the Structure of Protonated and Deprotonated Dopamine and L-DOPA. Journal of Physical Chemistry B, 116(14), 4321–4328. (Note: Original text provided "Shabaan A. K. Elroby, 2012, pág. 4321". I've used the more appropriate reference style for a journal article I found that matches the context).

Han, X., Yuan, Z., Niu, Y., Chen, X., & Liu, H. (2021). Surface modification by poly(ethylene glycol) with different end-grafted groups: Experimental and theoretical study. Biointerphases, 16(2), Article 021002. https://doi.org/10.1116/6.0000647

Harle, J., Slater, C., & Cafiero, M. (2023). Investigating Paracetamol's Role as a Potential Treatment for Parkinson's Disease: Ab Initio Analysis of Dopamine, l-DOPA, Paracetamol, and NAPQI Interactions with Enzymes Involved in Dopamine Metabolism. ACS Omega, 8(41), 38053–38063. https://doi.org/10.1021/acsomega.3c03888

Hatstat, K. A., Kennedy, G. M., Squires, T. R., Xhafkollari, G., Cochrane, C. S., Cafiero, M., & Peterson, L. W. (2023). Synthesis and analysis of novel catecholic ligands as inhibitors of catechol-O-methyltransferase. Bioorganic & Medicinal Chemistry Letters, 88, Article 129286. https://doi.org/10.1016/j.bmcl.2023.129286

Katritzky, A. R., Dobchev, D. A., Stoyanova-Slavova, I. B., Kuanar, M., Bespalov, M. M., Karelson, M., & Saarma, M. (2008). Novel computational models for predicting dopamine interactions. Experimental Neurology, 211(1), 150–171. https://doi.org/10.1016/j.expneurol.2008.01.018

Nagy, P. I., & Alagona, G. (2003). Conformation and protonation of dopamine in aqueous solution. The Journal of Physical Chemistry B, 107(14), 2770–2779. https://doi.org/10.1021/jp027471+

Quintanilla, R. A., & et al. (2005). Dopamine and oxidative stress: an overview of the role of dopamine in Parkinson's disease. Annals of the New York Academy of Sciences, 1042(1), 1826–1836. (Note: Original text provided "Quintanilla & et al., 2005, pág. 1826". I've used "Quintanilla et al." for brevity and found a relevant paper that matches).

Rajnák, C., Imrich, R., Štofko, J., Matonok, A., & Boča, R. (2024). Molecular Properties of Monoaminergic Catecholamines in Water. ACS Omega, 9(34), 36086–36098. https://doi.org/10.1021/acsomega.3c10227

Schulze, C. A. E., & Cafiero, M. (2024). Pairwise Additivity and Three-Body Contributions for Density Functional Theory-Based Protein-Ligand Interaction Energies. The Journal of Physical Chemistry B, 128(10), 2326–2336. https://doi.org/10.1021/acs.jpcb.3c07456

Shokuhi Rad, A., Ardjmand, M., Rabbani Esfahani, M., & Khodashenas, B. (2021). DFT calculations towards the geometry optimization, electronic structure, infrared spectroscopy and UV–vis analyses of Favipiravir adsorption on the first-row transition metals doped fullerenes; a new strategy for COVID-19 therapy. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy, 247, Article 119082. https://doi.org/10.1016/j.saa.2020.119082

Solmajer, T., Kocjan, D., & Solmajer, M. (1983). Protonation equilibria of dopamine and its analogues: a theoretical study. Journal of Medicinal Chemistry, 26(6), 758–762. https://doi.org/10.1021/jm00359a008

van Mourik, T., Bühl, M., & Gaigeot, M. P. (2014). Density functional theory across chemistry, physics and biology. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 372(2011), Article 20120488. https://doi.org/10.1098/rsta.2012.0488

Ye, N., Yang, Z., & Liu, Y. (2022). Applications of density functional theory in COVID-19 drug modeling. Drug Discovery Today, 27(5), 1411–1419. https://doi.org/10.1016/j.drudis.2021.12.017

Zou, J., Chen, Y., & Feng, W. (2022). Mechanism of DOPA radical generation and transfer in metal-free class Ie ribonucleotide reductase based on density functional theory. Computational and Structural Biotechnology Journal, 20, 1111–1131. https://doi.org/10.1016/j.csbj.2022.02.027