Analítica predictiva mediante regresión logística para la intervención temprana en ingeniería
Predictive analytics using logistic regression for early intervention in engineering
Casio Aurelio,
Torres López
![]()
![]() ; Jorge
Vladimir Pachas-Huaytan
; Jorge
Vladimir Pachas-Huaytan ![]() ; Jaime
Humberto Ortiz Fernandez
; Jaime
Humberto Ortiz Fernandez ![]()
Universidad Peruana Los Andes, Huancayo, Perú.
Resumen
El bajo rendimiento académico y la deserción estudiantil constituyen un problema crítico y costoso en las carreras de ingeniería, afectando la calidad educativa y la eficiencia institucional. Las métricas descriptivas tradicionales, ofrecen una visión retrospectiva insuficiente para la intervención temprana y proactiva. Por ello, se propone la integración de la Analítica Predictiva como una obligación gerencial para diagnosticar el riesgo académico de manera anticipada, se sostiene que la Regresión Logística (RL) es la técnica estadística idónea para este propósito. Así, se justifica por su solidez matemática para modelar resultados binarios (éxito/fracaso) y su capacidad para transformar una combinación de factores multidimensionales (académicos, psicosociales y socioeconómicos) en una probabilidad cuantificada acotada entre 0 y 1. Crucialmente, la RL permite la interpretación del Odds Ratio, un estadístico que traduce la complejidad en una métrica gerencial, cuantificando cuánto aumenta o disminuye la probabilidad de éxito de un estudiante por cada predictor. Esta interpretabilidad es vital para la toma de decisiones, permitiendo a los gestores universitarios priorizar recursos de intervención de forma costo-efectiva. La creación de un Sistema de Alerta Temprana con umbrales de riesgo diferenciados, guiando estrategias personalizadas de apoyo (tutoría intensiva, soporte socioemocional). Se concluye que la RL representa el balance óptimo entre la solidez estadística y la eficiencia gerencial, sirviendo como el estándar de interpretabilidad contra el cual deben compararse futuros modelos de Machine Learning más complejos, asegurando que la analítica se mantenga como una herramienta ética y de apoyo para la mejora de la trayectoria estudiantil.
Palabras Clave: regresión logística, rendimiento académico, deserción estudiantil, analítica predictiva, Odds Ratio, educación superior.
Abstract
Low academic performance and student dropout rates constitute a critical and costly problem in engineering programs, affecting educational quality and institutional efficiency. Traditional descriptive metrics offer an insufficient retrospective view for early and proactive intervention. Therefore, the integration of Predictive Analytics is proposed as a managerial imperative for diagnosing academic risk in advance. It is argued that Logistic Regression (LR) is the ideal statistical technique for this purpose. This is justified by its mathematical rigor in modeling binary outcomes (success/failure) and its capacity to transform a combination of multidimensional factors (academic, psychosocial, and socioeconomic) into a quantified probability bounded between 0 and 1. Crucially, LR allows for the interpretation of the Odds Ratio, a statistic that translates complexity into a managerial metric, quantifying how much each predictor increases or decreases a student's probability of success. This interpretability is vital for decision-making, allowing university administrators to prioritize intervention resources in a cost-effective manner. The creation of an Early Warning System with differentiated risk thresholds guides personalized support strategies (intensive tutoring, socio-emotional support). It is concluded that logistic regression represents the optimal balance between statistical robustness and managerial efficiency, serving as the standard of interpretability against which future, more complex machine learning models should be compared, ensuring that analytics remains an ethical and supportive tool for improving student outcomes.
Keywords: logistic regression, academic performance, student dropout, predictive analytics, odds ratio, higher education.
|
Recibido/Received |
17-06-2025 |
Aprobado/Approved |
25-11-2025 |
Publicado/Published |
26-11-2025 |
Introducción
La educación superior, y en particular las exigentes carreras de ingeniería, enfrentan un desafío crítico que impacta directamente en la calidad educativa y la eficiencia institucional: el bajo rendimiento académico y la consecuente deserción estudiantil (Pérez Obregón & Romero Díaz, 2018). Este fenómeno no solo representa una pérdida de potencial humano y una frustración individual para el estudiante, sino que también implica un gasto considerable de recursos para las universidades. En este contexto, la evaluación del rendimiento académico trasciende su función tradicional de mera calificación o registro histórico, transformándose en una herramienta estratégica indispensable para la gestión proactiva.
El costo de la deserción académica va mucho más allá de las cifras de matrícula. Se extiende a la pérdida de inversión estatal o privada por cada estudiante que abandona, a la sobrecarga de los servicios de apoyo y tutoría que fallan en la prevención, y a un ciclo negativo que afecta la reputación y los indicadores de eficiencia terminal de la institución. Las universidades, en su rol de formadoras de capital humano, tienen la responsabilidad estratégica de optimizar el proceso de aprendizaje, y esto comienza con la capacidad de diagnosticar el riesgo antes de que se convierta en una realidad irreversible. La meta es migrar de un modelo de control de daños a un sistema de prevención proactiva.
Tradicionalmente, las instituciones han confiado en métricas descriptivas, como el promedio de calificaciones (GPA), para diagnosticar el estado académico de sus estudiantes. Sin embargo, estas métricas, aunque necesarias, resultan insuficientes para identificar de manera anticipada a aquellos estudiantes que se encuentran en riesgo inminente de fracaso o abandono (Olani, 2017). El análisis puramente descriptivo ofrece una visión retrospectiva, limitando la capacidad de intervención temprana, que es precisamente donde reside la oportunidad de modificar trayectorias académicas negativas (Romero Basantes et al., 2025). La complejidad de este problema se ve amplificada por la irrupción de la sociedad digital, que demanda una rápida adaptación de los modelos educativos y tutorías, tanto en el uso de aulas virtuales (Ortiz Martínez et al., 2022) como en la integración de nuevas competencias y percepciones docentes (Gil-Fernández & Calderón-Garrido, 2023; Martín R. & García, 2018). La evidencia muestra que el rendimiento no solo está ligado a la inteligencia o la capacidad cognitiva, sino que es un fenómeno multifactorial profundamente influenciado por el entorno, la motivación y los recursos socioeconómicos del alumno.
Por consiguiente, se evidencia la necesidad imperante de evolucionar hacia sistemas de evaluación que incorporen la analítica predictiva. Esta evolución no es una opción tecnológica, sino una obligación gerencial. La analítica predictiva, al utilizar datos históricos y actuales, permite construir un Sistema de Alerta Temprana que genera una probabilidad de un evento futuro, como la reprobación o la deserción, con suficiente antelación para que los tutores y consejeros puedan actuar. La transición de un sistema reactivo, que simplemente documenta el fracaso, a uno predictivo, que lo anticipa y permite la acción, se ha convertido en una prioridad académica y de gestión (Fernández-Mellizo & Constante-Amores, 2020). Dicha transición se fundamenta en el uso de modelos estadísticos y de aprendizaje automático que puedan procesar un conjunto multidimensional de variables, que incluyen no solo el historial de notas, sino también factores sociodemográficos, hábitos de estudio, expectativas y autoeficacia (Nájera Saucedo et al., 2020).
Es en este marco conceptual donde la Regresión Logística (RL) emerge como una técnica estadística particularmente robusta y pertinente para el ámbito educativo. A diferencia de la regresión lineal, que busca predecir un valor continuo, la RL está diseñada específicamente para modelar la probabilidad de que ocurra un evento binario o dicotómico. En el contexto del rendimiento académico, esto se traduce en la capacidad de estimar la probabilidad de que un estudiante obtenga "éxito" o "fracaso" en una asignatura crítica, "continúe" o "abandone" sus estudios al final del semestre, o sea clasificado como estudiante "en riesgo" o "fuera de riesgo" (Pérez Pulido et al., 2023). La Regresión Logística, por su naturaleza, produce una salida probabilística inherentemente interpretable y acotada entre $0$ y $1$, lo que la hace directamente aplicable a la toma de decisiones.
El presente ensayo se plantea justificar la integración de la Regresión Logística como el eje central de un sistema moderno de evaluación del rendimiento en la educación superior, con un enfoque particular en las carreras de ingeniería. La idea central que se defiende es que la Regresión Logística es la técnica idónea y eficiente para este propósito, debido a su simplicidad analítica, su solidez matemática para resultados binarios y, crucialmente, su alta interpretabilidad a nivel de gestión. Al proporcionar valores concretos del Odds Ratio (OR), la RL permite a los gestores universitarios comprender no solo si una variable es predictiva, sino también cuánto aumenta o disminuye la probabilidad de éxito de un estudiante bajo ciertas condiciones (Dávila Cárdenes et al., 2015). El OR se convierte así en la métrica clave para priorizar recursos de intervención.
A lo largo de este análisis, se abordarán las limitaciones del modelo descriptivo tradicional y se establecerá una crítica fundamentada sobre la dependencia exclusiva del promedio como indicador. Posteriormente, se explorará la aplicación directa de la Regresión Logística en la gestión universitaria, discutiendo la selección de variables clave y la calibración de umbrales de probabilidad que permitan la activación de estrategias de intervención temprana y personalizada. Finalmente, se reflexionará sobre las implicaciones éticas de utilizar estos modelos para la toma de decisiones, asegurando que el enfoque se mantenga en el apoyo y la mejora de la trayectoria estudiantil, en consonancia con los objetivos de calidad y equidad en la educación superior (García-Berro et al., 2016). Este enfoque proactivo, sustentado por la evidencia estadística, es fundamental para garantizar la sostenibilidad de la matrícula y la excelencia educativa en el competitivo panorama de la formación de ingenieros en la actualidad (Acuña Torres et al., 2025; Serrano Montenegro et al., 2025).
Fundamento teórico y crítica al modelo descriptivo tradicional
El análisis predictivo en la educación superior requiere un marco teórico y metodológico que se ajuste a la naturaleza intrínseca del fenómeno que se pretende modelar. El rendimiento académico, especialmente cuando se evalúa en términos de retención o fracaso terminal, no es una variable continua, sino fundamentalmente dicotómica o binaria. El estudiante, al final de un ciclo, se clasifica en una de dos categorías mutuamente excluyentes: aprueba/suspende, continúa/abandona, o está en riesgo/no está en riesgo (Pérez Pulido et al., 2023). Esta realidad estructural hace que la Regresión Lineal Múltiple, la técnica de regresión más común para predecir variables continuas, sea inapropiada. La Regresión Lineal violaría los supuestos de normalidad y homocedasticidad de los errores, produciendo estimaciones sesgadas e ineficientes de los coeficientes (Pérez Obregón & Romero Díaz, 2018).
La crítica a la Regresión Lineal en este contexto binario se centra en tres fallas fundamentales. Primero, el supuesto de que el error del modelo (la diferencia entre el valor predicho y el valor real) sigue una distribución normal es violado, pues los errores solo pueden tomar dos valores posibles. Segundo, el problema de la heteroscedasticidad se vuelve severo, ya que la varianza del error no es constante, sino que depende del valor de las variables predictoras, lo que invalida los tests de significancia estadística. Tercero, y más importante a nivel práctico, la Regresión Lineal puede predecir valores de probabilidad que son matemáticamente absurdos, es decir, menores a cero o mayores a uno, lo que destruye la utilidad del modelo como herramienta de gestión.
La elección de la técnica predictiva es, por lo tanto, una decisión epistemológica que define la validez del estudio. Por el contrario, la RL se postula como el mecanismo estadístico por excelencia para abordar este tipo de modelización. Su principal virtud reside en la capacidad de transformar una combinación lineal de variables predictoras (factores académicos, personales, socioeconómicos) en una probabilidad cuantificada de que ocurra el evento de interés (éxito o fracaso).
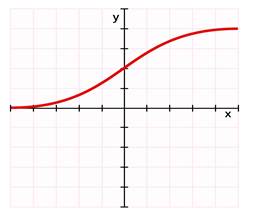
La RL logra esto mediante la función Logit, que es el logaritmo de las odds (la razón entre la probabilidad de que ocurra un evento y la probabilidad de que no ocurra, P/(1-P)). Al modelar el Logit como una función lineal de los predictores, y luego invertir esta transformación utilizando la función Sigmoide (o logística), la RL garantiza que el valor de salida siempre esté acotado en el intervalo [0, 1].
Figura 1. Curva de la función logística (sigmoide) y su mapeo de probabilidad
|
|
|
|
Esta función de enlace no lineal es la clave de su superioridad en el modelado de resultados binarios. La fórmula básica de la Regresión Logística garantiza la coherencia probabilística:
Logit (P) = ln (P/1-P) = β0 + β1X1 + β2X2 + βkXk
Donde P es la probabilidad de éxito, y β son los coeficientes que miden el cambio en el Logit por cada unidad de cambio en el predictor X. La RL, por tanto, resuelve el problema de la inadecuación de la distribución, permitiendo un análisis coherente y útil para la toma de decisiones y no requiere el estricto cumplimiento del supuesto de normalidad en la distribución de las variables predictoras (Romero Basantes et al., 2025).
Más allá de la mera clasificación, la ventaja gerencial y académica de la RL radica en la interpretación del Odds Ratio (OR). Este estadístico es el resultado de la exponenciación del coeficiente de regresión (OR = e β) y permite cuantificar la fuerza de la asociación entre cada predictor y la variable dependiente. El OR no solo indica la dirección del efecto (positivo o negativo), sino que también permite establecer una jerarquía de factores de riesgo o protección. Por ejemplo, si el OR de la variable "haber cursado un pre-universitario" es 1,8, se interpreta que los estudiantes que cursaron el pre-universitario tienen 1,8 veces las posibilidades relativas de éxito comparados con aquellos que no lo hicieron, manteniendo constantes el resto de las variables del modelo. Si el OR es inferior a 1 (ej., 0,60), indica que el predictor es un factor de riesgo que reduce las posibilidades de éxito. Por ejemplo, un OR de 0,60 para la variable "trabajar a tiempo completo" significa que las odds de éxito se reducen en un 40%.
Esta capacidad de medir el impacto diferencial de cada factor es fundamental para orientar los recursos de intervención de manera costo-efectiva. Los administradores pueden priorizar la acción sobre aquellas variables que tienen el mayor OR (positivo o negativo) y que, a su vez, son susceptibles de ser modificadas mediante políticas institucionales. La gestión se convierte en un ejercicio basado en la evidencia que optimiza el retorno de la inversión en programas de apoyo.
La adopción de la RL también sirve como crítica directa a la evaluación descriptiva tradicional. Si bien el Índice Académico (GPA) o promedio es un indicador potente y una variable de entrada obligatoria en cualquier modelo predictivo, su uso exclusivo ignora la influencia de determinantes no-cognitivos que son cruciales en la permanencia estudiantil. La crítica se centra en la falacia de que una única métrica puede encapsular la complejidad de la trayectoria estudiantil. Investigaciones demuestran que variables psicosociales como la autoeficacia percibida para el estudio, la claridad en el establecimiento de metas académicas (Nájera Saucedo et al., 2020), la procedencia educativa (Fernández-Mellizo & Constante-Amores, 2020) y las horas de dedicación al estudio tienen un peso significativo en el desempeño final. La RL permite integrar y ponderar estos factores sociodemográficos y motivacionales en un único modelo predictivo, ofreciendo una visión holística que la métrica promedio, por sí sola, es incapaz de proporcionar. Es más, la RL puede incorporar la naturaleza asimétrica del éxito académico; un modelo asimétrico de RL, por ejemplo, puede capturar mejor la probabilidad de resultados extremos, lo cual es de gran valor en la identificación de estudiantes en riesgo severo (Dávila Cárdenes et al., 2015).
Aplicación de la regresión logística en la gestión universitaria
La efectividad de un modelo predictivo se mide por su capacidad de generar acciones concretas y eficientes que impacten positivamente en la retención y el éxito académico. En la gestión universitaria contemporánea, el modelo de Regresión Logística debe ser el cimiento operativo de un sistema de alerta temprana diseñado para maximizar el retorno de la inversión institucional en apoyo estudiantil. Este modelo pasa de ser un ejercicio estadístico a convertirse en una herramienta táctica de apoyo pedagógico.
Selección de variables clave: En las carreras de ingeniería, la selección de predictores es crucial y debe basarse en la evidencia empírica que identifica los "filtros" académicos. Estos filtros son asignaturas de alta reprobación que actúan como puntos de inflexión en la permanencia del estudiante. Los modelos más eficaces no se limitan a las calificaciones globales, sino que discriminan entre tres categorías de variables:
· Variables pre-universitarias: Promedio de bachillerato y puntaje en exámenes de ingreso. Estas variables capturan el capital académico inicial del estudiante y su preparación previa (Fernández-Mellizo & Constante-Amores, 2020). Es fundamental incluir variables contextuales como el tipo de institución de procedencia (pública vs. privada) o la región geográfica.
· Variables intra-académicas: El rendimiento en las asignaturas secuenciales y cuantitativas iniciales, como Cálculo I, Cálculo II, Física I y Álgebra Lineal, es el predictor más potente. El fracaso o la suspensión de estas materias fundamentales durante el primer o segundo semestre se correlaciona fuertemente con la deserción posterior. El modelo de RL debe capturar el concepto de "dependencia secuencial"; es decir, no es solo la nota final, sino el número de veces que se ha reprobado una asignatura clave. La variable de "número de asignaturas suspendidas" en el primer ciclo es un predictor clave del riesgo de deserción (Olani, 2017).
· Variables personales y psicosociales: Horas dedicadas al estudio por semana, situación laboral o socioeconómica, y factores de autoeficacia, motivación intrínseca y estrategias de afrontamiento (Nájera Saucedo et al., 2020). La inclusión de estas variables no-cognitivas es lo que confiere a la RL su poder discriminante frente a los modelos descriptivos simples, ya que abordan la resiliencia y el compromiso del estudiante.
El diseño de este modelo se articula conceptualmente mediante la relación no lineal entre los factores de riesgo (X) y la probabilidad de un resultado binario (Y). La estructura del modelo permite a los gestores entender que la probabilidad de éxito no es una suma simple, sino una compleja interacción donde la falta de autoeficacia puede amplificar el impacto negativo de una nota baja en Cálculo I.
Validación y calibración del modelo: Un modelo predictivo, por excelente que sea su ajuste teórico, carece de utilidad gerencial si no está debidamente validado y calibrado. Es imperativo medir la capacidad predictiva y discriminatoria del modelo mediante métricas como la Curva ROC (Receiver Operating Characteristic) y el Área Bajo la Curva (AUC). La Curva ROC representa gráficamente la relación entre la sensibilidad (tasa de verdaderos positivos) y la especificidad (tasa de verdaderos negativos) del modelo para todos los posibles umbrales de probabilidad. Un valor de AUC cercano a 1,00 indica una capacidad predictiva casi perfecta, mientras que un valor de 0,50 indica un rendimiento equivalente al azar. La obtención de un AUC alto (típicamente superior a $0,75$) proporciona la confianza necesaria para que la gestión universitaria base sus decisiones en estos resultados.
Asimismo, la calibración implica determinar el punto de corte óptimo de probabilidad (Pcorte) que equilibre la sensibilidad y la especificidad, optimizando así los recursos de intervención. Este punto no siempre es 0,50; si el costo de un "falso negativo" (no identificar a un estudiante en riesgo) es muy alto, se podría optar por un Pcorte más bajo (ej., 0,40) para aumentar la sensibilidad, asumiendo una mayor tasa de "falsos positivos" (identificar a estudiantes fuera de riesgo que en realidad no lo están). Esta decisión táctica es clave en la gestión de la intervención temprana.
Estrategias de intervención temprana: La Regresión Logística proporciona un valor de probabilidad (P) que permite establecer umbrales de riesgo diferenciados, transformando la predicción en una estrategia escalonada de intervención. La asignación de recursos debe ser proporcional al nivel de riesgo detectado por la probabilidad calculada:
· Riesgo Alto (Priesgo> 0,70): Intervención de soporte psicológico/tutoría intensiva y remedial. Estos estudiantes deben ser contactados de forma prioritaria y proactiva, idealmente a través de un sistema de tutoría personalizada donde el tutor (Ortiz Martínez et al., 2022) asuma un rol de mentoría integral. La intervención debe ser remedial en lo académico (cursos de refuerzo en asignaturas filtro) y de soporte socioemocional, abordando factores de autoeficacia y manejo del estrés, dado que su probabilidad de fracaso o abandono es estadísticamente inminente y su inacción representa el mayor costo potencial para la institución.
· Riesgo Medio (0,50 < Priesgo < 0,70): Monitoreo y tutorías específicas de asignatura o talleres de habilidades blandas. La intervención aquí se enfoca en reforzar competencias académicas específicas, a menudo mediante el uso de recursos digitales y laboratorios de refuerzo. Es el grupo ideal para talleres sobre gestión del tiempo, técnicas de estudio o manejo de la ansiedad ante exámenes. El seguimiento debe ser constante, con reportes trimestrales de avance, para evitar la escalada al nivel de riesgo alto.
· Riesgo Bajo (Priesgo = 0,50): Seguimiento rutinario y fomento de la excelencia. La intervención se enfoca en el mantenimiento del desempeño y en la promoción de oportunidades de liderazgo, mentoría o becas, reforzando el comportamiento exitoso y contribuyendo a un clima académico positivo, convirtiéndolos en potenciales mentores de sus pares en riesgo.
Implicaciones éticas y de gestión: La aplicación de estos modelos conlleva una profunda responsabilidad ética y requiere una gestión institucional robusta. Es imperativo que el resultado del modelo de RL se utilice exclusivamente como una herramienta de apoyo y nunca de exclusión o estigmatización del estudiante. La revelación de la probabilidad de riesgo a los estudiantes debe manejarse con sensibilidad, enfocándose siempre en el plan de acción y no en el diagnóstico predictivo per se. La gobernanza de datos debe ser transparente y asegurar la privacidad de la información predictiva, cumpliendo con todas las normativas de protección de datos personales.
El foco debe estar en la mejora de la trayectoria y en la personalización del apoyo, asegurando que la analítica predictiva contribuya a los objetivos de equidad y no se convierta en una política punitiva (García-Berro et al., 2016). Esto implica la necesidad de capacitar al personal (tutores, docentes y personal administrativo) no solo en el uso de las herramientas de software, sino también en la interpretación ética de los resultados estadísticos (Gil-Fernández & Calderón-Garrido, 2023). Deben entender que el modelo predice una probabilidad, no un destino. Finalmente, el compromiso requiere la asignación de recursos presupuestarios sostenibles para sostener las estrategias de intervención derivadas del modelo, dado que la inversión en la retención estudiantil ha demostrado ser significativamente más rentable a largo plazo que la constante captación de nuevos alumnos. La integración de la RL es, por tanto, una decisión que fusiona la excelencia académica con la responsabilidad social universitaria.
La RL como fundamento estratégico
El desafío de la retención y el éxito académico en la educación superior, particularmente en los complejos planes de estudio de ingeniería, exige una ruptura definitiva con los métodos de evaluación meramente descriptivos. La conclusión ineludible de este análisis es la reafirmación de que la RL es una herramienta esencial para la modernización y la dotación de valor predictivo y estratégico a los sistemas de evaluación universitaria. La Regresión Logística, al abordar la naturaleza inherentemente dicotómica del riesgo académico, proporciona una solución estadística robusta que supera las deficiencias de la regresión lineal tradicional. Su poder no reside únicamente en la capacidad de clasificar a los estudiantes, sino, de manera crucial, en la generación de una probabilidad cuantificada de riesgo que permite la toma de decisiones basada en la evidencia.
La fortaleza analítica de la RL se manifiesta en la interpretación del Odds Ratio. Este coeficiente es el lenguaje que traduce la complejidad estadística en información gerencial útil, al cuantificar el impacto preciso de cada factor predictor (académico, psicosocial, o socioeconómico) en las posibilidades relativas de éxito. Al conocer el peso específico de variables como el rendimiento inicial en asignaturas cuantitativas o el nivel de autoeficacia, las instituciones pueden dejar de lado las intervenciones genéricas para enfocarse en la modulación de las palancas de cambio más influyentes. Esto transforma el análisis de datos de un simple ejercicio de recopilación a un motor de inteligencia institucional, alineando los recursos de apoyo estudiantil con las necesidades reales y proyectadas de la población de riesgo. En esencia, la RL dota a la gestión universitaria de una visión de futuro, permitiendo que la universidad se adelante al fracaso en lugar de limitarse a registrarlo.
1. Llamada a la acción: Integración de la analítica predictiva
Instamos enfáticamente a las instituciones de ingeniería y a las facultades con altas tasas de deserción a dar el paso decisivo hacia la integración total de la analítica predictiva en sus políticas de retención. Adoptar la Regresión Logística como estándar operativo implica un compromiso institucional a tres niveles: tecnológico, humano y financiero.
A nivel tecnológico, es imperativo establecer plataformas de business intelligence que automaticen la recopilación de datos de múltiples fuentes (historiales académicos, encuestas de ingreso, registros de actividad en aulas virtuales) y que ejecuten el modelo de RL con periodicidad trimestral. Esto garantiza que la identificación de riesgo sea dinámica y en tiempo real, permitiendo la activación de las estrategias de intervención temprana detalladas en este ensayo. La eficiencia de los recursos se dispara cuando se establece un sistema de umbrales claro, como el esquema de riesgo Alto (Priesgo > 0,70) y Medio (0,50 < Priesgo < 0,70), que dirige la tutoría intensiva (soporte psicológico y académico) solo a aquellos que tienen la mayor probabilidad de fracaso, liberando recursos para intervenciones más ligeras en el segmento de riesgo moderado.
Sin embargo, el éxito de la analítica predictiva no reside en el algoritmo, sino en la voluntad política y la capacitación del personal. La implementación efectiva de un sistema basado en la Regresión Logística requiere una inversión sostenida en la formación de tutores y directivos, asegurando que comprendan la lógica estadística detrás de la probabilidad de riesgo. Es crucial desmitificar el modelo, enfatizando que se trata de una herramienta de apoyo y no de un mecanismo de exclusión. La ética de la gestión de datos debe ser el principio rector, garantizando que la información predictiva se maneje con la máxima privacidad y siempre con el objetivo final de apoyar, mentorizar y guiar al estudiante hacia el éxito. Es un imperativo moral y de eficiencia; invertir en retención es, a largo plazo, la estrategia financiera más sólida para cualquier institución educativa que busque la excelencia y la estabilidad de su matrícula. La universidad debe asumir su rol como agente de cambio, utilizando la ciencia de datos para equilibrar la equidad (identificando a quienes más necesitan apoyo) con la calidad (manteniendo altos estándares académicos).
2. Futuras Vías: La Evolución de los Modelos Predictivos
Aunque la Regresión Logística ha demostrado ser la solución más interpretable y pragmática para la gestión de riesgo académico a nivel administrativo, el campo de la analítica de datos en educación avanza rápidamente, ofreciendo futuras vías de investigación que deben explorarse con rigor. El próximo paso en la sofisticación de los modelos predictivos pasa necesariamente por la comparación exhaustiva de la RL con modelos de Machine Learning más complejos.
Entre estos modelos se destacan los Árboles de Clasificación, los Bosques Aleatorios (Random Forests) y las Máquinas de Soporte Vectorial (SVM). Estos modelos avanzados tienen el potencial de capturar interacciones no lineales entre las variables predictoras (ej., que el efecto del promedio de bachillerato cambie en función de la autoeficacia), lo que podría, teóricamente, incrementar la precisión predictiva (aumentar el valor AUC). Por ejemplo, los Árboles de Clasificación ofrecen una ruta de decisión visualmente clara, aunque a menudo sacrifican la interpretabilidad de los coeficientes (como el Odds Ratio) por una mayor capacidad de ajuste a los datos.
La investigación futura debe centrarse en un estudio comparativo riguroso, evaluando tres métricas clave:
1. Precisión Predictiva (AUC): Determinar si el incremento en la exactitud de los modelos de ML avanzados justifica su complejidad.
2. Robustez y Generalización: Evaluar cómo se comportan los modelos (RL vs. ML) al ser aplicados a cohortes de estudiantes distintas a la cohorte de entrenamiento.
3. Interpretabilidad para la Toma de Decisiones: Medir la facilidad con la que el personal de tutoría puede traducir los resultados del modelo en acciones concretas.
Es fundamental que la comunidad académica y de gestión de ingeniería mantenga la Regresión Logística como el benchmark de interpretabilidad. Solo si un modelo de Machine Learning demuestra una ventaja sustancial y estadísticamente significativa en la precisión predictiva, y si se pueden desarrollar herramientas que traduzcan su complejidad a un lenguaje gerencial comprensible (por ejemplo, mediante la explicación de la importancia de la característica o feature importance), se debería considerar su adopción. Mientras tanto, la Regresión Logística se erige como el balance óptimo entre la solidez estadística, la eficiencia gerencial y el compromiso ético de apoyar proactivamente a los estudiantes en su camino hacia la excelencia profesional.
Agradecimientos
A nuestra universidad.
Conflicto de intereses
No se reporta.
Referencias
Acuña Torres, L., Alvarado Trujillo, A., & Rivas del Águila, M. P. (2025). Leer en tiempos digitales: Experiencias y percepciones de estudiantes de primaria sobre la lectura con herramientas tecnológicas. e-Revista Multidisciplinaria del Saber, 3, e-RMS01062025. https://doi.org/10.61286/e-rms.v3i.218
Dávila Cárdenes, N., García-Artiles, M. D., Pérez-Sánchez, J. M., & Gómez-Déniz, E. (2015). Un modelo de regresión logística asimétrico que puede explicar la probabilidad de éxito en el rendimiento académico. Revista de Investigación Educativa, 33(1), 27–45. https://doi.org/10.6018/rie.33.1.178481
Fernández-Mellizo, M., & Constante-Amores, A. (2020). Determinantes del rendimiento académico de los estudiantes de nuevo acceso a la Universidad Complutense de Madrid. Revista de Educación, 387, 213–240. https://doi.org/10.4438/1988-592X-RE-2020-387-433
García-Berro, E., Roca, S., Navallas, F. J., Soriano, M., & Ras, A. (2016). El impacto de las políticas de evaluación del profesorado en la posición en los ránquines universitarios: El caso de la Universidad Politécnica de Cataluña. Aula Abierta, 44(1), 23–30. https://doi.org/10.17811/rifie.44.01.2016.23-30
Gil-Fernández, R., & Calderón-Garrido, D. (2023). Percepción de los docentes ante los retos de la sociedad digital. Bordón. Revista de Pedagogía, 75(4), 93–108. https://doi.org/10.13042/Bordon.2023.97600
Martín Rodríguez, D., & García, M. (2018). Transformación del modelo educativo en el aprendizaje y desarrollo competencial: Estudio de caso. Bordón. Revista de Pedagogía, 70(4), 103–119. https://doi.org/10.13042/bordon.2018.60992
Nájera Saucedo, J., Salazar Garza, M. L., Vacío Muro, M. de los Ángeles, & Morales Chainé, S. (2020). Evaluación de la autoeficacia, expectativas y metas académicas asociadas al rendimiento escolar. Revista de Investigación Educativa, 38(2), 435–452. https://doi.org/10.6018/rie.350421
Olani, A. (2017). Predicción del éxito académico de estudiantes durante el primer año de universidad. Electronic Journal of Research in Educational Psychology, 7(19), 1053–1072. https://doi.org/10.25115/ejrep.v7i19.1351
Ortiz Martínez, E., Santos Jaén, J. M., & Gras Gil, E. (2022). Educación superior y tutoría: Uso del aula virtual en contabilidad. Digital Education Review, 42, 16–33. https://doi.org/10.1344/der.2022.42.16-33
Pérez Obregón, J. M., & Romero Díaz, T. (2018). Análisis del rendimiento académico mediante regresión logística y múltiple. Revista Electrónica de Conocimientos, Saberes y Prácticas, 1(2), 33–42. https://doi.org/10.30698/recsp.v1i2.10
Pérez Pulido, M. O., Mejía Ardila, O. C., Serrano Novoa, C. A., Suescún Garcés, S. J., & León, F. J. (2023). Analysis of academic performance from a binary logistic regression model (O. Mogollon-Alaguna, Trans.). Innovaciencia, 11(1). https://doi.org/10.15649/2346075X.3423
Romero Basantes, M. B., Saransig De La Torre, Y. C., Aguilar Reyes, J. E., Morocho Barrionuevo, T. P., & Mejía Peñafiel, E. F. (2025). Evaluación comparativa de la regresión y los árboles de clasificación para identificar los factores determinantes en el rendimiento académico de los estudiantes de nivelación en la carrera de estadística. Reincisol, 4(7), 3601–3634. https://doi.org/10.59282/reincisol.V4(7)3601-3634
Serrano Montenegro, Y., Solís, O. A., & Ramírez Mendoza, P. N. (2025). Influencia de las competencias digitales en el rendimiento académico y la evolución curricular del inglés universitario panameño. e-Revista Multidisciplinaria del Saber, 3, e-RMS10042025. https://doi.org/10.61286/e-rms.v3i.210
(1)